Discrete Math 🔢
Lets get the math straight
Computers perform computations. Most of us are acquainted with the abstractions represented through data structure and programming language features. Yet beneath those layers lies math and logic encoded.
The most intuitive question you may ask at first is:
How is discrete math different from the continuous one?Discrete math deals with countable sets. It is a set whose elements are finitely describable. Integers would fall in this category as there is a sharp distinction between subsequent numbers/objects. Continuous math, on the other hand, involves real numbers with decimal values (gradient difference). As you will see in future, we need to make special adjustments to deal with fractional values in computers.
Hence, discrete math is the approach computers take. Data is stored in discrete bits (and bytes). In the coming sections, we will cover the key concepts, the journey so far, research happening today, and how to stay updated in future developments.
Key concepts
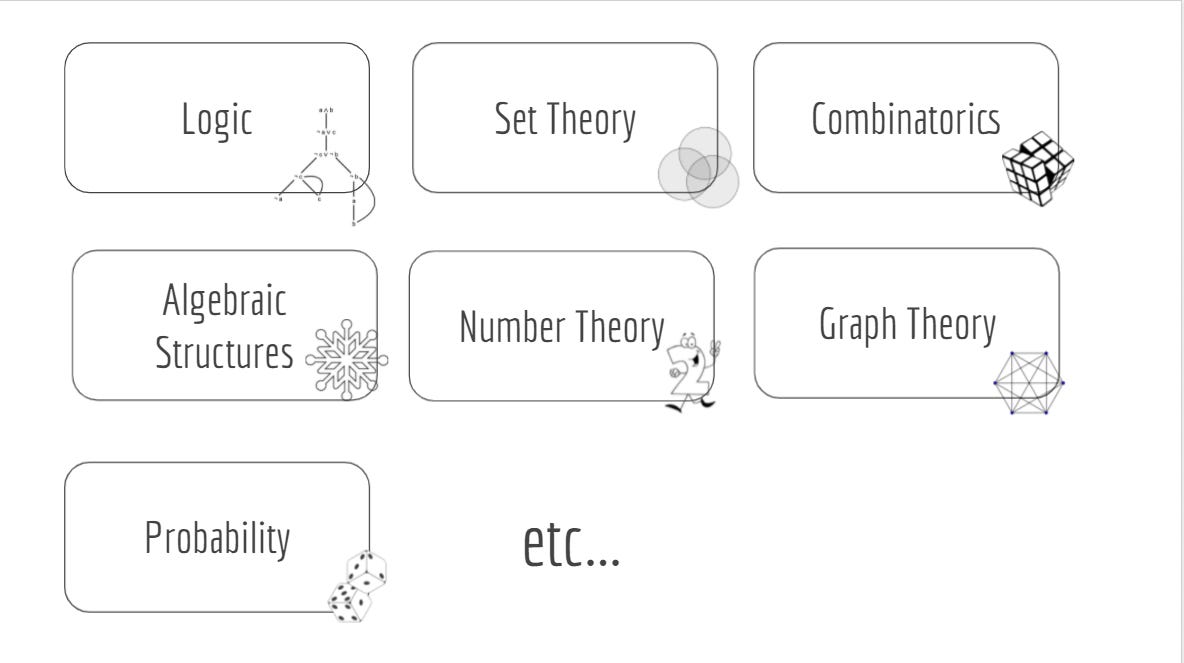
Logic is all about representing information in a suitable abstraction involving statements and applying laws (such as De Morgan’s) to simply it as needed. Set Theory categorizes objects as sets and carries out actions on top of it. Combinatorics deals with arrangement of these objects.
Graph Theory tends to focus on the interconnectivity between them. Algebraic Structures deal with set representations with special properties which gradually built atop each other. It even extends to geometry when we illustrate the concepts on a multidimension surface.
Moving to connected fields in math, we have game theory where study is done to predict decisions by players of a system - based on their discrete variables in question (eg: Prisoners Dilemma). In fact, given the convenience of dealing with values that are discrete, discretization is an approach taken to convert continuous values.
Journey thus far
The field developed as humanity tried to tackle different problems. One of those was the four color theorem in graph theory (1850’s) where the challenge is to prove a map (like the world map) can distinctively color each section to distinguish it from the adjacent ones - using only 4 colors. Set Theory by Georg Cantor has both solved abstraction challenges yet opened up several new problems.
In the more recent past, number theory was extensively studied for encryption during the world war - as well for decryption. Development on this front more or less happened to solve long standing problems and its branching topics.
Present Day work
Within the scope of computer science, discrete math is essential in developing algorithms, functionalities in programming languages (eg: monoids in Haskell), cryptography (number theory concepts), theorem proving systems (eg: Coq, Lean), and general software development abstractions.
In the scope of math research, there is quite a bit of literature to digest to better understand the varied research that’s happening. One researcher in particular that interests us is Peter Scholze’s work which shows promise for the coming decades.
Since discrete math plays such a pivotal role in the foundations of computer science, you can expect every major development in pure math will have a translated impact in our domain subsequently.
How to get involved?
If these points pique your interest and you wish to delve deeper on related topics, you can consider the following resources that helped us get our fundamentals clear:
Quanta Magazine - math related posts
If you want to test the waters in a fun manner, we would highly recommend going through the problems listed in the book: To guard and art gallery and other discrete math adventures. In each chapter, you are posed an interesting problem and gradually challenged to develop the intuition to structure the problem and develop an abstraction.
We had fun in the chapter on jugs to measure certain liters of water. From a computer science/programming scope, it will take time for you to grasp the fundamentals to see how it takes shape in programming language abstractions so we do not proactively recommend getting hands-on immediately. But curiosity has no safety rails for the inquisitive ones so if you discover new resources, do let us know.
Credits: Nithin S Sabu for the slides, and thorough research on related topics for our learning sessions.
In the next post, we will cover about a subset of Discrete Math that specially interests Joel - Graph Theory & Combinatorics. You can expect a wide ranged analysis of graphs both in its structure and application.
Until then, 👋



Neat round up!